Vector and tensor tomography

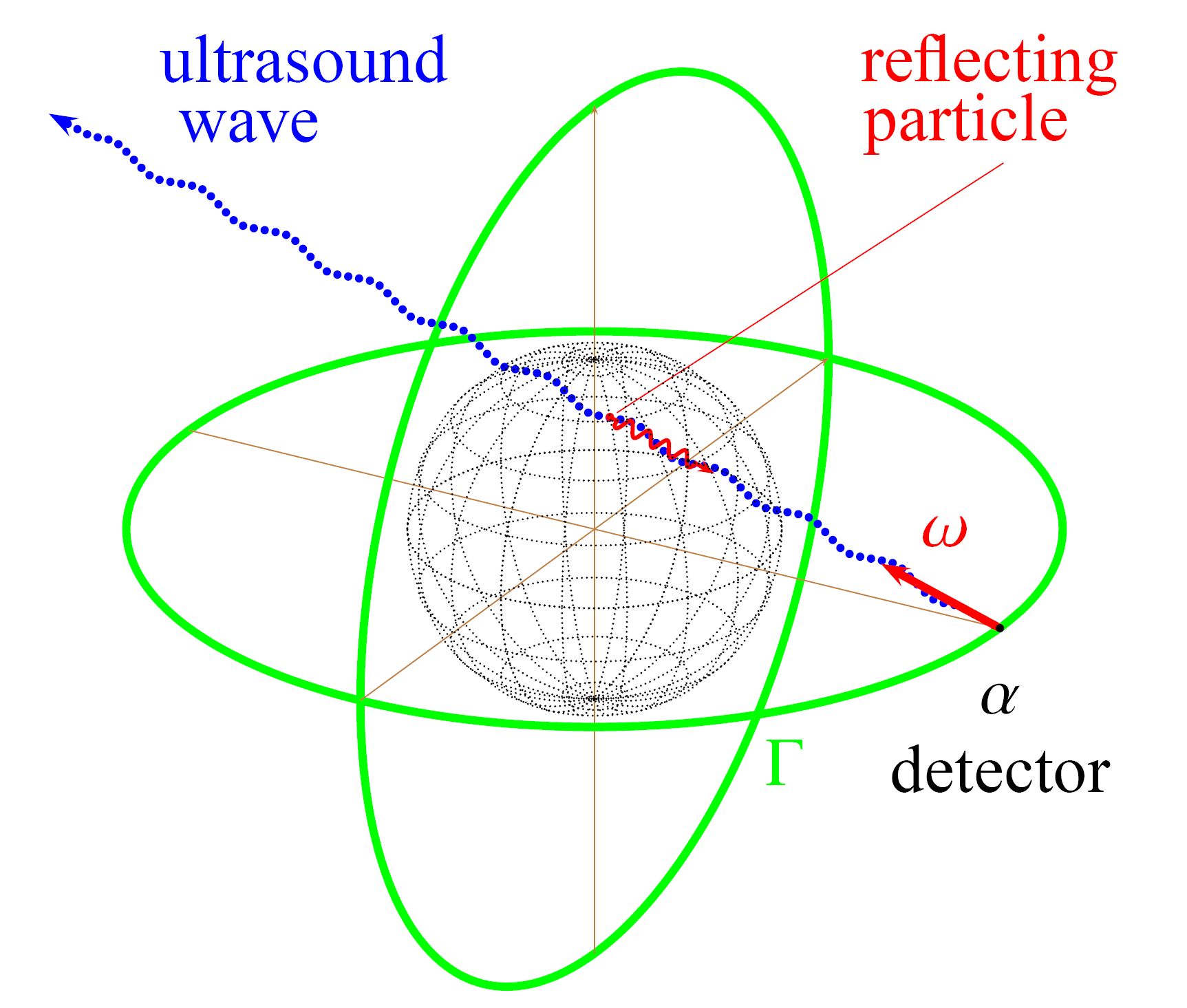
Mathematical models for vector and tensor tomography problems are usually given as integrations of the fields with respect to geodesic curves in a Riemannian manifold. The integral operators are called ray transforms. In the simplest case the metric is the Euclidean one and the geodesics are straight lines. An equivalent formulation is given as inverse source problem for a transport equation where the differential operator is the geodesic vector field and the boundary values are given by the measured data. Since the data are scalar functions, the underlying inverse problems are underdetermined, which means that the ray transforms have a non-trivial null space. This is one significant difference to classical computerized tomography, since the Radon and X-ray transforms are injective. There are challenging analytical and numerical problem such as:

• Range characterization of the transforms
• Continuity and differentiability of the forward operators
• Development of (approximate) inversion formulas
• Stable and efficient numerical solvers for general Riemannian metrics
• Investigation of vector and tensor fields that depend on time
• Simultaneous computation of the field and the underlying metric
• Inclusion of attenuation

Currently the project is performed in close cooperation with Prof. Alfred K. Louis from Saarland University (as further principal investigator), Prof. Bernadette Hahn from the University of Würzburg as well as with a Russian team from the Sobolev Institute of Novosibirsk (Russia) led by Prof. Dr. Evgeny Y. Derevtsov and is funded by the German Science Foundation (DFG) under SCHU 1978/19-1 and  LO 310/17-1.

There are very interesting topics in the framework of this project for bachelor and master theses. Please do not hesitate to contact us.